O OLHO DA PROVIDÊNCIA (1) NO SIMBOLISMO MAÇÔNICO

Sérgio Koury Jerez

Diferentemente de alguns dos símbolos adotados na maçonaria, como o compasso, o esquadro e outros que notadamente são artefatos criados pelo homem e de uso corrente na maçonaria operativa, o Olho da Providência contido dentro de um triângulo é, em si mesmo, um símbolo de símbolos, que procura, de um modo peculiar, nos transmitir a idéia de onisciência do Grande Arquiteto do Universo.

Para entendê-lo – e nesse particular ele se comporta como os demais símbolos – é preciso que empreendamos uma longa viagem ao passado, embora saibamos que sua origem real estará sempre além, nos confins do tempo, da capacidade humana de documentar idéias.

Egípcios, acádios, assírios e babilônios

Começamos, como qualquer pesquisador que queira entender a simbologia adotada pelas sociedades ocidentais, a procurar as raízes do Olho da Providência nas civilizações antigas, em especial na egípcia e suas contemporâneas da Mesopotâmia. E, na nossa caminhada, vamos acabar por constatar que em todas as culturas originárias daquela região, como as dos assírios, babilônios e acádios, além dos próprios egípcios, reverenciava-se um deus que era representado por um anel alado.

Anel alado Assírio (foto tirada no Museu Britânico por Robin Edgar)

Parece haver consenso entre os estudiosos de que o anel alado é uma referência ao Sol, que cruza os céus do oriente ao ocidente, “voando sobre a Terra” como se tivesse asas.

Há uma hipótese um pouco mais elaborada, mas nem por isso destituída de fundamento, de que o anel alado representaria o eclipse do sol. A julgar pela foto abaixo, isso é bem plausível. E, se assim for, é possível que uma derivação do anel alado (e do eclipse que ele representaria) tenha dado origem à lenda da Fênix. Mas essa é uma outra história…

Eclipse do Sol, foto de Steve Albers

Ao longo dos mais de cinco mil anos de história do Egito antigo, o símbolo do anel alado passou por algumas mutações e o anel foi gradualmente deixando de ter a forma primitiva para se transformar em um olho.

O Olho alado egípcio (foto tirada no Museu Britânico por Robin Edgar, em agosto de 1999)

Talvez tenha sido nessa mesma época que, para os egípcios, o olho passou a ser um atributo da deusa Maat . [2]

Maat (ou ma’at), filha de Ra [3] , o Deus-Sol, era, para os antigos egípcios, o conceito da verdade, justiça e equilíbrio. Os juízes, por exemplo, eram considerados sacerdotes de Maat.

Sentada no Salão de Julgamento de Osíris, Maat julgava as almas dos mortos. O olho de Maat podia ver tudo e era com base nesse poder que a deusa decidia se, pelos atos praticados, o recém-falecido tinha ou não o direito a uma nova oportunidade de vida e qual seria ela. Sem Maat, portanto, o processo de criação e de renovação do Eu, que era parte da tradição egípcia, ficaria comprometido.

Com o tempo, porém, Maat acabou emprestando seu símbolo a Horus, e o olho passou a ser associado àquele deus.

Duas versões do Olho de Horus

A lenda de Horus

Horus era um dos mais importantes deuses egípcios. Um deus-sol representado como um falcão, ou como um homem com cabeça de falcão, cujo olho direito representava o Sol e, o esquerdo, a Lua.

O olho direito de Horus: o Sol O olho esquerdo simbolizava a Lua

Diz a lenda que durante a batalha com Set para vingar o assassinato de Osíris, seu pai, Horus teve seu olho arrancado e cortado em pedaços. Depois da vitória, o olho foi recomposto por Thot .[4]

O símbolo era um amuleto poderoso. Considerava-se que trazia sabedoria, saúde e prosperidade. O olho era pintado em barcos e outros objetos pedindo proteção divina. Jóias representando o olho eram colocadas com os mortos e pintadas nos sarcófagos. Era chamado de udjat ou utchat.

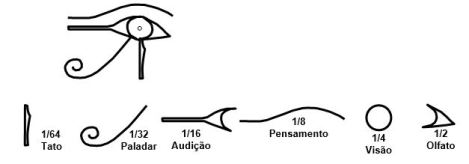
O Olho de Horus tinha um significado muito peculiar. Era representado como uma figura com 6 partes, que correspondiam a seis sentidos – Tato, Paladar, Audição, Pensamento, Visão, Olfato. O olho era o receptor e processador desses sentidos. Algo assim como se tivesse as funções que hoje em dia atribuímos ao cérebro.

Sua construção seguia leis muito precisas. Os sentidos eram ordenados de acordo com sua importância e de acordo com quanta energia deveria “alimentar” o olho para que um indivíduo recebesse uma determinada sensação. Todos os dados sensoriais eram “alimentos”.

À partir de aproximadamente 1200 a. C., o sistema de medida egípcio passou a adotar o Olho de Horus para representar um sistema de quantificação fracionária. 

.

O olho inteiro media 1 heqat. E cada uma das partes do olho media frações do heqat.

Estas eram as partes do Olho de Horus e as frações e sentidos [5] correspondentes:

Pitágoras e a Trindade

Filósofo e matemático grego nascido no ano de 580 a.C na cidade de Samos, Pitágoras deixou sua terra natal para escapar da tirania de Polícrates e foi para o sul da Itália em aproximadamente 518 a.C. (antes, segundo alguns). Iamblico, um de seus maiores biógrafos, dá outras razões para sua partida e faz um comentário sobre a resposta dos samianos aos métodos pedagógicos usados pelo sábio:

“… ele tentou usar seu método simbólico de ensinar que era similar em todos os aspectos às lições que ele havia aprendido no Egito. Os samianos não eram muito afeitos a esse método e o trataram de maneira rude e imprópria.”

Em Croton (hoje Crotona), Pitágoras fundou uma ordem ou escola filosófico-religiosa que teve muitos seguidores. Seus discípulos mais próximos eram conhecidos como mathematikoi.

Os mathematikoi viviam permanentemente na escola, não tinham posses pessoais e eram vegetarianos. Usavam como símbolo uma estrela de cinco pontas que era marcada em suas mãos. Obedeciam regras rígidas e eram ensinados pelo próprio Pitágoras, que defendia que:

• no seu nível mais profundo, a realidade é o número (e, por extensão, a matemática) aplicado à natureza;

• a filosofia pode ser usada para a purificação espiritual;

• a alma pode elevar-se e unir-se ao divino;

• certos símbolos têm uma significação mística, e;

• todos os irmãos da ordem deveriam observar lealdade rígida e segredo.

Não obstante seus biógrafos atribuam seu nome a uma homenagem a Pítia, profetiza do templo de Apolo, em Delfos, mais a palavra ágora, que significa lugar (de pessoas), me atrevo a sugerir uma outra etimologia para ele. Segundo o Houaiss, ágora é a praça principal das antigas cidades gregas, local em que se instalava o mercado e que muitas vezes servia para a realização das assembleias do povo; formando um recinto decorado com pórticos, estátuas etc., era tb. um centro religioso. A ágora ἀγορά, também “assembleia”, “lugar de reunião”, derivada de ἀγείρω, “reunir” é um termo grego que significa a reunião de qualquer natureza, geralmente empregada por Homero como uma reunião geral de pessoas. Parece ter sido uma parte essencial da constituição dos primeiros estados gregos.

Como é sabido, Pitágoras, ainda jovem, percorreu a maior parte do mundo civilizado daquela época colhendo os conhecimentos que seriam a base para seus futuros ensinamentos. Concentrou-se especialmente no Egito e de lá trouxe certamente tudo o que se poderia saber então sobre a arte de construir, ainda que, é bom que se diga, a nação que um dia tivera Ramsés II como faraó já não vivesse seus dias de maior esplendor.

Foi lá, provavelmente com os sacerdotes do deus Ptah – deus egípcio dos construtores, arquitetos, pedreiros, escultores, artesãos, ferreiros e artistas – que Pitágoras tomou contato com as técnicas de divisão da circunferência que levou para a Grécia, assim como deve ter sido nos templos de Horus que aprendeu as noções de retidão, justiça e de saúde que transmitia a seus discípulos.

Como Ptah é não só o deus, mas o conjunto de qualidades inerentes a ele, todos os discípulos de Ptah encarnavam, pela prática de seus conhecimentos, o próprio deus. Dessa forma, como o sábio grego teria se tornado, quando no Egito, um discípulo de Ptah, era, ele mesmo, um Ptah. Assim, por haver criado um centro de estudos onde repassava os conhecimentos que obteve dos egípcios, é razoável supor que seu nome seja proveniente das ágoras em devoção a Ptah, tornando-se, por isso, Pitágoras..

Pitágoras

Tudo o que se sabe de Pitágoras nos foi transmitido por terceiros, seus discípulos ou não. Um fato curioso é que as particulares relações entre os lados do triângulo retângulo, cujo teorema leva o seu nome e pelo qual ganhou fama, já eram conhecidas 1.000 anos antes de seu nascimento, pelos babilônios.

Pitágoras interessava-se por todas as questões inerentes ao homem, ao universo e à natureza de forma geral. Foi ele, por exemplo, quem percebeu que a órbita da Lua era inclinada no equador da Terra e foi também um dos primeiros a constatar que uma determinada estrela que era vista durante o anoitecer nada mais era do que Vênus, a estrela d’alva.

O que era fundamental para Pitágoras era a autenticidade do auto-conhecimento, a fim de que este fosse aplicado para o bem dos outros homens através do ensinamento santo e sagrado relativo à Tríade divina .[6]

Por meio do estudo dos polígonos, Pitágoras deu-se conta de que Deus tinha uma lógica para a criação de cada coisa. Bastava descobri-la.

A questão da Tríade ou Trindade como um símbolo de Deus pode ser explicada da seguinte forma:

1) Os pitagóricos (discípulos de Pitágoras) certamente acreditavam que o Grande Arquiteto do Universo, na sua perfeição, jamais iria criar algo que não fosse originalmente perfeito.

2) Julgavam que apenas os polígonos regulares [7] eram perfeitos;

3) Acreditavam que era possível criar qualquer figura geométrica regular utilizando, para tanto, apenas os pontos contidos no círculo;

4) Provavelmente, pensavam que a circunferência era uma metáfora do universo, onde a Origem era representada pelo ponto central [8] ;

5) Perceberam, também, que nenhum polígono pode ser criado dentro do círculo apenas com o ponto central, nem tampouco com o ponto central e mais outro ponto, já que dois pontos podem ser antagônicos [9] . Mas que, com três pontos, subitamente era revelada a glória da criação e nascia o mais simples e fundamental dos polígonos regulares: o triângulo equilátero.

6) Concluíram que o terceiro ponto é que justificava os outros dois, já que, para que houvesse a criação – e, portanto, para que o Criador também passasse a existir [10] – os três se tornavam mutuamente necessários, sem qualquer hierarquia entre eles.

Pontos são “apenas” pontos, por definição.

Para que exista a circunferência é necessário um ponto central. Para que o triângulo eqüilátero seja criado – ou seja, para que se realize a criação inicial, que precede todas as outras – são necessários três pontos ou, metaforicamente, três Forças Criadoras que poderíamos chamar, por exemplo, de Sabedoria, Força e Beleza ou Pai, Filho e Espírito Santo.

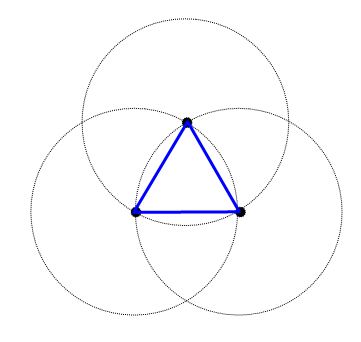
Os pitagóricos possivelmente as representavam assim através do desenho geométrico:

São três circunferências essencialmente iguais, indiferenciadas, da mesma forma que o são os três pontos centrais que lhes dão Origem. Os pontos são indistintos, porque não há como distinguir pontos. Quem conhece um conhece todos e quem conhece todos conhece apenas um. São iguais entre si. Podemos chamá-los de a, b e c, mas isso não os individualizará. Dado um ponto, jamais saberemos se é o a, o b ou o c. Não um ponto no papel, é claro; mas um ponto no espaço, no “éter”, na mente de um ser humano. Um ponto que é uma abstração, como é uma abstração qualquer idéia que se faça de Deus.

O triângulo, ou criação fundamental, é emanado dos três pontos sem que haja prevalência de qualquer um deles. Mas somente a junção dos três propicia a criação. Portanto, são os três que constituem a força única, o Criador, capaz de gerar o universo e todos os seus seres. Os três juntos são Um, o Único que é capaz de criar.

É esse triângulo, responsável pela existência simultânea de Criador e Criatura, que os pitagóricos reverenciavam e que o cristianismo adotou como seu.

A solução de Rinaldini e a Vesica Pisces

Desde as civilizações antigas o homem busca fórmulas gerais para a divisão da circunferência [11] . Os primeiros de que se tem notícia nessa busca foram os sacerdotes egípcios. Mas eles eram iniciados, e as técnicas construtivas que desenvolviam eram segredos que compartilhavam apenas com seus iguais e com seu deus Ptah. O pouco que se sabe sobre o que descobriram é pela análise de suas obras.

Depois, já com os filósofos e matemáticos gregos, a começar pelo próprio Pitágoras, a geometria foi se popularizando. Mas, talvez pelo fato dos matemáticos gregos não utilizarem pontos localizados fora do círculo para criar polígonos, não chegou aos nossos dias nenhuma teoria daquela época que fosse genérica, capaz de permitir a divisão do círculo em qualquer número de partes.

Somente no século XIII, Etienne Tempier, bispo de Paris, que condenava várias das proposições dos filósofos helênicos, desenvolveu uma solução para o problema, que até hoje faz parte dos currículos escolares. Carlo Rinaldini (1615-1698) e Nicolas Bion (1652-1733), também estudaram a questão e lançaram, cada um deles, processos que permitiam dividir o círculo em um número qualquer de partes, sendo o de Rinaldini considerado o melhor dos três.

Não vamos aqui detalhar o processo de Rinaldini, mas julgamos essencial apresentar sua aparência para que se perceba do que estamos falando.

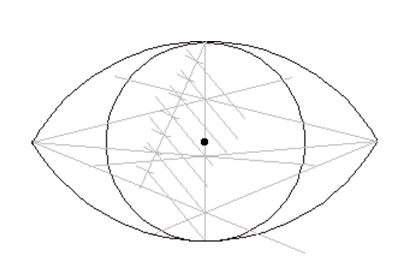
A solução de Rinaldini para a divisão da circunferência

Curiosamente, como o leitor certamente já terá deduzido, a utilização da solução de Rinaldini é, no seu cerne, guardadas as proporções, comparável à do Olho de Horus para a divisão do inteiro em várias frações.

Um outro fato interessante é que, para obter sua solução, Rinaldini, que certamente conhecia bem o que chamamos de geometria sagrada, recorreu à Vesica Pisces [12] – muito utilizada pelos artistas do renascimento e pelos construtores dos arcos góticos – que é uma figura formada pela intersecção de duas circunferências que se tocam nos respectivos centros, como se vê na figura abaixo:

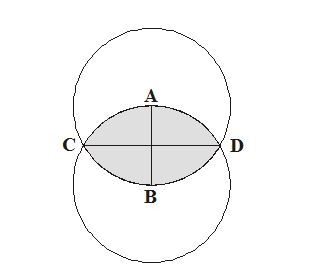
A Vesica Pices (área hachurada) tem uma propriedade que é muito particular: da relação entre os segmentos AB e CD nasce a raiz quadrada de 3, o que nos remete novamente à instigante natureza da trindade.

Detalhando um pouco mais, temos que:

Se dois círculos compartilham o mesmo raio (AB), sua intersecção cria a Vesica Pisces, onde CD dividido por AB é igual à raiz quadrada de 3, que é igual a 1,732.

A Vesica Pisces tem inúmeras conotações e correlações, boa parte delas dentro da tradição cristã, mas também está relacionada às pirâmides, astronomia, cabala etc.

Conclusão

Cremos que, por tudo o que os estudos de Pitágoras e seus discípulos representaram para o desenvolvimento das técnicas construtivas e para a evolução da humanidade, é razoável supor que o Olho da Providência contido no triângulo, e que é adotado como símbolo maçônico, tenha sido uma justa homenagem a quem, como eles, buscou incessantemente uma solução geral para a divisão da circunferência. Foram, não só por isso, mas também pelo conjunto de suas idéias, de fundamental importância para o aparecimento da nossa ordem. Como grande estudioso da geometria, no que tange a dividir o círculo em partes iguais, Rinaldini, que viveu mais de 2.000 anos depois de Pitágoras, talvez possa ser considerado o seu mais destacado discípulo, pois concluiu com êxito e perfeição a obra que o sábio e revolucionário mestre grego iniciou.

O símbolo do olho omnividente, no entanto, aparentemente jamais deixou de ser usado. Segundo S. Brent Morris, Past Master da loja Patmos no 70, de Ellicott City, Maryland, E.U.A. “Era parte da iconografia cultural popular nos séculos XVIII e XIX. Como foi durante esse período que o ritual e o simbolismo maçônico evoluiu, não é surpresa que muitos dos símbolos comuns e conhecidos pela sociedade em geral tenham sido levados para as cerimônias maçônicas. Em 1614, por exemplo, o frontispício de ‘A história do mundo’, de Walter Raleigh, mostrava um olho numa nuvem com o título de ‘Providentia’.”

Aquele que parece ter sido o primeiro uso “oficial” do Olho da Providência pela maçonaria, se deu (embora sem mencionar o triângulo) na publicação The Freemasons Monitor, quase 100 anos depois da morte de Rinaldini. Dizia, então, Thomas Smith Webb a esse respeito: “E embora nossos pensamentos, palavras e atos possam ser ocultados dos olhos dos homens, o Olho-que-tudo-vê, ao qual o Sol, a Lua e as estrelas obedecem, e sob cujo atento cuidado os cometas fazem suas estupendas revoluções, penetra nos recessos mais interiores do coração humano e nos recompensará de acordo com os nossos méritos”

Coincidência ou não, quatorze anos antes, os fundadores dos Estados Unidos da América já o tinham utilizado no Grande Selo da então nova nação, embora dos quatro homens que participaram da elaboração daquele brasão apenas Benjamin Franklin fosse maçom.

Devemos lembrar, estando nossa tese correta, é claro, que foram agregados ao desenho de Rinaldini alguns traços para que, efetivamente, ele corresponda à anatomia de um olho humano. Mas essa qualidade “humana”, me parece, não faz jus àquele a quem o símbolo realmente quer representar. Mesmo porque, o que de fato representaria o Grande Arquiteto do Universo nessa simbologia não é o olho como um todo, mas sua pupila. Além do triângulo, é claro!

Embora os templos do Palácio Maçônico, em São Paulo, exibam o triângulo contendo um olho esquerdo, nas pesquisas realizadas nada foi descoberto que pudesse indicar essa preferência. No entanto, parece haver um certo consenso entre estudiosos de que o olho representado dentro do triângulo deveria ser o da onisciência ou onividência, também chamado de olho frontal ou “terceiro olho”, com o qual a solução de Rinaldini parece ter mais identidade.

Para finalizar este artigo, talvez valha a pena fazer um apanhado geral de algumas das coisas que o Olho da Providência envolto pelo triângulo potencialmente representa: o Sol, a Lua, a onisciência do Grande Arquiteto do Universo, a verdade, a justiça e o equilíbrio, o retorno à vida pela reencarnação (eis a fênix mais uma vez), os sentidos, a justa medida, a prosperidade, a lógica do pensamento divino, a trindade, os cristãos, a saúde, a essência da criação e, do ponto de vista estritamente geométrico, a maravilhosa possibilidade de divisão do círculo em partes iguais, que, em última análise, tem sido a responsável pelo progresso da humanidade. É realmente fantástico que um único símbolo contenha em si todas essas idéias!

Mas, para quem se dedica a entender a geometria sagrada, esse símbolo guarda ainda uma última mensagem, talvez a mais especial, qual seja: Tudo emana do centro, do ponto central onde todas as coisas existem, em estado latente, pela vontade do Grande Arquiteto do Universo, esperando ser tornadas reais pela mente e obra humanas.

[1] Providência. [do lat. Providentia.] S.f. 1. A suprema sabedoria com que Deus conduz as coisas. 2. P.ext. O próprio Deus. 3. Prudência e presciência do futuro para acautelamento com relação a ele. …

[2] Maat, Ísis, Osíris, como Amon, Ptah, Horus etc., não eram, efetivamente, deuses ou deusas. Eles eram o que os egiptólogos chamam de neter, ou seja, aspectos, funções, atributos de um Único e Supremo Deus. O neter, erroneamente traduzido como deus ou deusa, era a personificação de energias, poderes, forças que, através de suas ações e interações criaram, mantiveram e continuavam a manter o universo.Não obstante, continuaremos a utilizar a denominação deus ou deusa ao longo deste artigo, por julgarmos que o leitor está mais familiarizado com ela do que com neter.

[3] Às vezes também, nas lendas egípcias mais antigas, confundido com Horus

[4] Thot ainda usou de magia para restaurar uma parte do olho, referente a 1/64, que havia sido perdida.

[5] Existem associações e deduções interessantes feitas com base nas relações entre sentidos e frações. Vide,por exemplo, na Internet, http://www.aloha.net/~hawmtn/horus.htm ou http://www.sangraal.com/library/eyesofhorus.htm

[6] Pitágoras acreditava que a própria Tríade não poderia ser compreendida a não ser que se considerasse sua relação com o Ponto. O Ponto, por sua vez, não poderia ser captado senão como Um com relação à Díade. E a Mônada e a Díade não poderiam ser completamente entendidas a menos que também fossem vistas em termos da Tríade. E assim as séries de números prosseguiam.

[7] Que possui todos os lados congruentes e todos os ângulos congruentes.

[8] Nesse aspecto, é intrigante como a teoria do Big Bang, respeitadas as diferenças de objetivo, é uma cópia mais elaborada da forma de pensar dos pitagóricos.

[9] “Mas toda tensão entre opostos culmina em liberação, da qual surge o “terceiro”. No terceiro, a tensão é resolvida e a unidade perdida é restaurada.” Carl G. Jung

[10] Pois sem criatura não existe criador e vice-versa.

[11] É preciso lembrar, nesse particular, que a procura por soluções desse tipo era considerada – como até hoje pode ser – uma busca para entender a forma de pensar do Grande Arquiteto do Universo. Ou seja, dividir a circunferência para que se possa criar todos os tipos de polígonos regulares é um dos primeiros passos rumo à compreensão da Suprema Inteligência.

[12] Do latim. Que, em português, significa bexiga de peixe.

Bibliografia

—————————

Aslan, Nicola – Estudos Maçônicos Sobre Simbolismo – Rio de Janeiro, Ed.Aurora

Boucher, Jules – A Simbólica Maçônica – São Paulo, Ed. Pensamento.

Campbell, Joseph – As Máscaras de Deus – São Paulo, Ed. Palas Athena, 1992.

Campbell, Joseph – O Poder do Mito – com Bill Moyers, 1a edição, 2a reimpressão, São Paulo, Ed. Palas Athena, 1991.

Cirlot, Juan-Eduardo – Dicionário de Símbolos – São Paulo, Ed. Moraes Ltda, 1984.

Ferreira, Aurélio Buarque de Holanda – Novo dicionário da língua portuguesa – 1a edição, 15a impressão, Ed. Nova Fronteira, Rio de Janeiro.

Gebara, Ivone – Trindade, palavra sobre coisas velhas e novas: uma perspectiva ecofeminista – São Paulo, Paulinas, 1994.

Hawking, Stephen – Uma breve história do tempo: do Big Bang aos buracos negros – Rio de Janeiro, Ed. Rocco Ltda, 1988.

Hawking, Stephen – O Universo numa casca de noz – São Paulo, Ed. Mandarim, 2001.

Iyer, Raghavan – Pythagoras and his school – Santa Barbara, Concord Grove Press, November 1977 – http://theosophy.org/tlodocs/PitágorasandHisSchool.htm

Morris, S. Brent – The eye in the pyramid – http://www.srmason-sj.org/council/journal/dec99/morris.html

O’Connor J. J. e Robertson E. F. – Pythagoras of Samos –

http://turnbull.dcs.st-and.ac.uk/~history/Mathematicians/Pythagoras.html

Putnoki, José Carlos – Elementos de Geometria e Desenho Geométrico vol.II – São Paulo, Ed. Scipione Ltda, 1991

Schuré, Édouard – Os Grandes Iniciados – São Paulo, IBRASA, 1985

REIS MAGOS, ZOROASTRISMO E MAÇONARIA

Tradução José Filardo

Por Yves Bomati

Em 6 de janeiro, a Epifania celebra os três reis magos vindos do Oriente para prestar homenagem ao Cristo, recém-nascido em Belém. A viagem deles não é questionada, mesmo se a festa que ela gera consista na partilha alegre de um bolo de “Reis”. O que é a “Epifania”? Quem são estes magos guiados por uma estrela? E em que este episódio está relacionado com a maçonaria?

A Epifania e os Magos do Oriente

Doze dias depois do Natal, a Epifania, palavra que significa, segundo a etimologia grega, “aparição”, marca o retorno percebido da luz após o solstício de inverno. Que vêm, portanto, fazer ali os Reis Magos, nem hebreus, nem gregos, nem romanos, na lenda cristã?

O apóstolo Mateus (2,1-12) indica que eles chegam do Oriente guiados por uma estrela, sem dar mais detalhes. Não foi senão a partir do século VI que se fixará o seu número e seus nomes Caspar, Melchior e Baltazar, e que lhes será atribuída uma tripla origem, Asiática, europeia e Africana, para promover a universalidade almejada do cristianismo.

A verdade é mais direta. Quando do nascimento de Cristo, os únicos magos orientais conhecidos eram os Medos, originários do império persa, o atual Irã. Eles praticavam o zoroastrismo, a forma reformada do mazdaismo, e eram especialistas na ciência dos astros. Sem a estrela brilhante que os teria guiou, eles certamente não teriam empreendido uma viagem de mais de 1.600 km com o único propósito de depositar ouro, incenso e mirra aos pés de um recém-nascido. A sua missão é mais fundamental: eles vieram legar ao cristianismo e ao novo mundo, por seu gesto simbólico, o melhor de sua religião, proporcionando uma ponte entre suas próprias crenças e o primeiro cristianismo que a permeará amplamente.

A riqueza moral do zoroastrismo

O Avesta, escrito por vários séculos é o livro sagrado dele. Seus textos mais antigos, os Gathas, prosódias de lirismo cósmico, são devidos ao profeta Zaratustra (também conhecido como Zoroastro pelos europeus), e datam do século XVII aC.

Zaratustra é um “reformador-filósofo”. Antes de sua pregação, o mazdeismo, religião de Ahura Mazda, resultou de um amálgama de velhas crenças, incluindo a coexistência de múltiplas divindades. Entre elas, Mitra parece ocupar um lugar proeminente. A ele se sacrificavam animais, enquanto que durante a sua adoração se consumia uma bebida energética feita de efedra, a haoma. Ao lado dele, outros deuses garantiam as colheitas, nascimentos, fertilidade dos casamentos, as estações do ano, etc. O fogo (Atar), o símbolo da incorruptibilidade era comemorado em todos os lugares.

É esse politeísmo que Zaratustra tem a intenção de reformar. Mudando o foco da divindade para as leis, ele reverencia apenas o princípio primeiro, o ordenador, Ahura Mazda, rejeitando os deuses, deixando subsistir as noções ou abstrações relacionados a eles. O zoroastrismo mais puro vai além das tradições, redefine a relação entre as pessoas e o princípio soberano, o pensamento que o sustenta trazendo com ele uma revolução social e espiritual.

Ahura Mazda é o Único. Conceito espiritual que não pode ser representado, ele é onisciente e onipotente. Ele tem seis atributos, herdados dos antigos deuses, solidariedade mútua, o Amesha Spenta (“as forças imortais que fazem progredir”) e interfere na evolução do mundo. O homem, chamado a desempenhar um papel ativo em seus desígnios, usa suas energias superiores para acessar o Bom Pensamento, a Boa Palavra e a Boa Ação. Esta colaboração entre o homem e o princípio superior é necessária em virtude da luta incessante entre as forças da vida (o bem, a inteligência, a luz) e a não-vida (o mal, o obscurantismo e a escuridão). O homem é livre para escolher entre a duas, mas deve arcar com as consequências.

Esta é uma pequena parte da mensagem revolucionária, ordenadora e moral que Zaratustra oferece à humanidade e que faz dele o fundador do monoteísmo mais antigo do mundo.

A influência de Zoroastro sobre os fundamentos da Maçonaria Europeia

Sua mensagem somente penetra na Europa na virada do século XVIII. Na verdade, as Viagens na Pérsia de Tavernier (1605 – 1689) e depois de Chardin (1643 -1713) onde são evocados os ritos de Guebres – outro nome dos zoroastristas – e a imagem de Zoroastro, guia dos Magos, despertar o interesse dos intelectuais. A moda é lançada: a tradução do Avesta, parcial, e completa em seguida, as obras que aparecem em 1700 em Oxford e depois em 1702 em Paris, onde Pierre Bayle (1647-1706) acrescenta um artigo sobre Zoroastro em seu Dictionnaire historique et critique, aumentando consideravelmente a influência do zoroastrismo sobre as correntes emergentes de pensamento.

Ramsay, Cahusac, Mozart… e outros

O Cavaleiro de Ramsay, bem conhecido nas lojas maçônicas, capturou a temática em 1727 e produziu um romance bem-sucedido As Viagens de Ciro e logo após um Discurso sobre a Mitologia que tornam ainda mais popular o profeta-filósofo. A batalha se trava entre os sábios: para alguns, o zoroastrismo permanece em uma visão de mundo “dualista” campo de batalha entre o bem e o mal; para outros, incluindo Ramsay, ele carrega consigo um monoteísmo cósmico cujas consequências perturbariam a ordem religiosa. Segundo Jean-Noël Laurenti, “o ensinamento emprestado de Zoroastro tendia a reconhecer um Deus único, e lhe conferia um lugar essencial entre dois princípios, o bem e o mal. Como o parentesco de tal religião com o cristianismo era flagrante, e que assim Zoroastro era considerado mais velho que Moisés, a tentação era grande de concluir que o cristianismo representava apenas uma forma entre outras de um monoteísmo acessíveis todos os homens, independentemente da Revelação. (…) Zoroastro se tornaria, assim, uma figura emblemática do deísmo. ” Não estamos no coração dos fundamentos da Maçonaria?

A mania por Zoroastro se estende a todas as artes. Jean-Philippe Rameau criou em 1749 uma tragédia lírica Zoroastro, reconstruída em 1756 e repetida com grande sucesso. Ele escolheu como libretista Louis Cahusac, secretário do conde de Clermont, Grão-Mestre da Grande Loja da França em 1742, que “defende bastante abertamente os ideais maçônicos, com uma história abordando a batalha da luz contra as trevas, que ilustra o hino ao sol, Mil Raios Brilhantes (ato 3, cena 5)”.

Mozart, em 1791, amplia ele também em A Flauta Mágica, a personagem de Zaratustra, sob os traços e acentos de Sarastro, em um contexto maçônico ainda mais presente. Ao contrário de seus antecessores, ele foi capaz de compreender melhor a essência do Zoroastrismo graças à primeira tradução completa francesa do Avesta. De fato, em 1757, Anquetil Du Perron (1731-1805) reencontrou os Parsis de Bombaim, descendentes dos zoroastristas iranianos que fugiram ao domínio árabe do século IX, que provocou a islamização das terras iranianas e trouxe uma cópia do misterioso Avesta . Ele publica assim, traduzido, em 1771 o Zend-Avesta, um livro de Zoroastro contendo as ideias teológicas, físicas e morais do legislador, as cerimônias do culto religioso que ele estabeleceu e várias características importantes relacionadas com a história antiga dos persas.

Contra todas as probabilidades, algumas mentes se decepcionaram com o que descobriram. Voltaire dedica um artigo irônico em seu Dicionário Filosófico: “Não se pode ler duas páginas do lixo abominável atribuído a Zoroastro, sem sentir pena da natureza humana. Nostradamus e o médico das urinas são pessoas razoáveis comparados a esse energúmeno; e mesmo assim falamos sobre ele, e voltaremos a falar. ”

Voltaire estava certo em sua última frase. Não se parará de falar de Zaratustra e seus pensamentos iluminados, livre da escória que o tempo fez pesar sobre ele.

Assim, Zaratustra, é uma das chaves do pensamento iraniano, também moldou o pensamento maçônico no século XVIII, sem ofensa a Voltaire. Sua filosofia moral, diferente da que Nietzsche revelou em Assim Falava Zaratustra, continua a ser, acima de tudo uma ode à felicidade e um caminho em direção a melhor viver em sociedade, longe das trevas. Nossos Reis Magos da Epifania não seriam o elo que continua a nos unir hoje a ele? Sua palavra original, em todo caso, sempre ilumina o pavimento de mosaico, ao mesmo tempo em que guia os homens para o Bom Pensamento, a Boa Palavra e a Boa Ação, quando ele escreve nos Gathas:

“Oh! Ahura Mazda
Zarathustra segue o caminho de teus pensamentos
mais evolutivos e produtivos para o mundo.
Que pela irradiação da Justiça e da ação que emana do Pensamento justo,
nossa vida material e espiritual tome força
e que a Serenidade ilumine
nosso mundo interior
e nos leve a uma vida feliz.”

(Os Gathas, canto VIII, Yasna, hat 43)

O MANUSCRITO COOKE

O Manuscrito Cooke (texto integral)

Traduzido do espanhol por José Antonio de Souza Filardo M .´. I .´.

O Manuscrito Cooke é a fonte de onde se elaborou a lenda de Hiran.

Damos graças a Deus, nosso glorioso Pai, Criador do Céu e da Terra e tudo o que nela está e que ele conhece [em virtude] de sua Gloriosa Divindade.

Ele fez todas as coisas para ser obedecido, e muitas delas em benefício da humanidade, lhes ordenou submeterem-se ao homem, porque todas as coisas que são comestíveis e de boa qualidade [servem] para o sustento do homem.

E também deu ao homem inteligência e habilidade em várias coisas, e arte, por meio da qual podemos viajar por este mundo para assegurar a sobrevivência, para fazer muitas coisas para a Glória de Deus e também para o nosso benefício e paz de espírito.

Se tivesse que enumerar todas essas coisas, levaria muito tempo para dizer e escrever.

Mostrarei uma delas, embora deixe outras: Isto é, a forma como começou a Ciência da Geometria, e quem foram os criadores dela e de outras Artes, conforme revelado na Bíblia e outras histórias.

Vou narrar, como disse, como e de que modo começou e esta ciência digna da Geometria.

Você deve saber que existem sete Ciências Liberais e, logo saberá por que são chamadas dessa forma, e porque destas primeiras sete se originam todas as Ciências e Artes do mundo e, especialmente, porque aquela, a Ciência da Geometria é a origem de todas.

Quanto à primeira, que é chamada de fundamento da Ciência, é a Gramática, que ensina o homem a falar e escrever de forma justa.

A segunda é a Retórica, que ensina o homem a falar decorosamente de maneira precisa.

A terceira é a Dialética, e que ensina o homem a discernir o verdadeiro do falso, e é comumente chamada de Arte ou [Filosofia].

A quarta é chamada aritmética, e ensina aos homens a arte dos números, para calcular e contar todas as coisas.

A quinta é a Geometria, que ensina aos homens os limites e a medida e ponderação dos pesos de todas as Artes humanas.

A sexta é a Música, que ensina aos homens a Arte do canto nas notas da voz e do órgão, da trompa, da harpa e todos os demais instrumentos.

O sétimo é a Astronomia, que ensina ao homem o curso do Sol e da Lua e de outros planetas e estrelas do Céu.

Nosso principal objetivo é tratar do primeiro fundamento da excelente Ciência da Geometria, e de quem foram seus fundadores; como disse anteriormente, há sete Ciências Liberais, ou seja, sete artes ou ciências, ou Artes que são livres em si mesmas, as quais vivem apenas por meio da Geometria.

E a Geometria é, como se diz, a medida da Terra: “Et sic dicitur a geoge pin Px ter a Latine e metrona quod est mensura.

Unde Geometria i mensura terre vel Terrarum”, ou seja, que a Geometria é, como eu disse, Geo, terra, e metron, medida e, assim, o nome Geometria é composto, e se chama medida da Terra.

Não se maravilhe que eu tenha dito que todas as Ciências vivem só pela Ciência da Geometria, porque nenhuma delas é artificial [que pressuponha, como a Geometria, o Artífice].

Nenhum trabalho que o homem faça é realizado, a não ser por meio da geometria; uma razão importante: Se um homem trabalha com as mãos e, trabalha então com qualquer tipo de utensílio, e não há qualquer instrumento feito de coisas materiais deste mundo que não venha da Terra e à Terra retorne, e não existe qualquer instrumento, ou seja, utensílio de trabalho, que não tenha proporções.

E proporção é medida, e utensílio ou instrumento, é Terra.

Por isso, pode-se dizer que os homens deste mundo vivem através do trabalho de suas mãos.

Muitas outras provas eu te dei sobre a razão pela qual a Geometria é a Ciência da qual vivem todos os homens razoáveis, mas desta vez não deixarei o longo processo da Escritura.

E agora prosseguirei com a minha tese; você compreenderá que, entre todas as Artes do mundo, a [mais importante] é a Arte do Homem; a Arte da construção tem a maior importância e a maior parte na Ciência da Geometria, conforme está escrito e dito na história, na Bíblia, e no Polycronicon, uma crônica ilustrada e na História de Beda, em De Immagine Mundi e no Ethimologiarum de Isidoro, em Metodio, bispo e mártir, e em muitos outros; digo que a Maçonaria é a principal [Arte] da Geometria, como penso que pode se dizer por que foi a primeira a ser criada; como se diz na Bíblia, no Livro I do Gênesis, Capítulo 4.

E também todos os Doutores mencionados o dizem, e alguns deles mais aberta e simplesmente [com relação], ao que é dito na Bíblia.

O Filho direto da linhagem de Adão, descendente das sete gerações de Adão antes do dilúvio, foi um homem chamado Lameth, que tinha duas mulheres; da primeira, Ada, teve dois filhos: um chamado Jabal e outro Jubal.

O mais velho, Jubal, foi o primeiro fundador da Geometria e da Construção, e construiu casas e é chamado na Bíblia de “pater habitancium in tentoriis atque pastorum”, ou seja, o pai dos homens que vivem em tendas, ou seja, em casas.

E foi professor de Caim e chefe de todos os seus trabalhadores quando construiu a Cidade de Enoch, que foi a primeira cidade jamais construída, e que Caim entregou a seu filho e a chamou Enoch.

E agora é chamada Efraim.

E a Ciência da Geometria e da Maçonaria foi primeiramente inventada e utilizada como Ciência e Arte, e, portanto, poderíamos dizer que foi a origem e o fundamento de todas as Artes e Ciências, e este homem, Jabal, foi chamado “Pater pastorum”.

O mestre da História e Beda, De Immagine Mundi, Polycronicón e muitos outros dizem que, pela primeira vez ele fez a distribuição da Terra, de modo que cada homem poderia individualizar (conhecer) seu campo e seu trabalho.

E também dividiu rebanhos e ovelhas, e por isso podemos dizer que foi o primeiro fundador dessa Ciência.

E seu irmão Jubal, ou Tubal foi o fundador da Música e do canto, como afirma Pitágoras no Polycronicón e mesmo Isidoro em suas Etimologias; em seu livro I diz que foi o primeiro fundador da música e do canto, do órgão e da trompa, e que encontrou a ciência do som através dos golpes dos metais, graças a seu irmão Jubalcaín.

A Bíblia diz na verdade no capítulo IV do Gênesis, que Lameth teve um filho e uma filha com outra mulher chamada Zillah.

Seus nomes eram Tubalcaím, o filho e a filha foi chamada Naamah, e com diz o Polycronicón, era a esposa de Noé; se isto é verdade ou não, não sabemos.

Eu lhe digo que este filho, Tubalcaín, foi o fundador da Arte da Metalurgia e de todas as Artes dos metais, ou seja, do ferro, do ouro e da prata, como dizem alguns Doutores, e sua irmã Naamah foi fundadora da Arte da Tecelagem, fiavam o fio e trabalhavam o ferro e faziam vestimentas como podiam, mas a mulher Naamah encontrou a arte da tecelagem, que agora é chamada de Arte das Mulheres; e estes três irmãos sabiam que Deus se vingaria do pecado e com o fogo ou com a água, e colocaram o máximo cuidado para salvar as Ciências que haviam encontrado e se aconselharam entre si; e graças à sua engenhosidade, disseram que havia dois tipos de pedra de tal qualidade que a primeira jamais podia ser queimada, e esta pedra é chamada mármore, e que a outra pedra não podia ser derretida, e esta pedra era chamado laterus.

E, por isso, tiveram a ideia de escrever todas as ciências que tinham encontrado nestas duas pedras, de modo que se Deus se vingasse com fogo o mármore não se queimaria, e se Deus se vingasse com a água a outra pedra não se derreteria.

E por isso pediram ao irmão mais velho de Jabal que construísse duas colunas com estas duas pedras, ou seja, mármore e laterus, e que esculpisse nos dois pilares todas as Ciências e a Artes que tinham encontrado.

E assim foi feito e, por isso podemos dizer que eles foram muito hábeis na ciência que se iniciou e que prosseguiu até ao seu final antes do dilúvio de Noé; sabendo que a vingança de Deus iria ocorrer, seja por fogo ou água, os irmãos – em uma espécie de profecia – sabiam que Deus ordenaria uma delas e por isso escreveram nas duas pedras as sete Ciências, pois achavam que a Vingança chegaria.

E ocorreu que Deus se vingou e aconteceu tal dilúvio que todo o mundo ficou submerso e morreram todos, menos oito pessoas.

Eles foram Noé e sua esposa e seus três filhos e suas esposas, e destes filhos se originou todo o Mundo.

E [os três filhos] foram chamados assim: Sem, Cam e Japhet.

E este Dilúvio foi chamado Dilúvio de Noé, porque só se salvaram ele e seus filhos.

E muitos anos depois do Dilúvio, como narra a Crônica, estas duas colunas foram encontradas, e como diz o Polycronicón, um grande doutor chamado Pitágoras encontrou uma, e Hermes, o filósofo encontrou a outra, e ensinaram as ciências que encontraram escritas nelas.

Qualquer crônica, a história e muitos outros documentos e, sobretudo a Bíblia testemunham a construção da Torre de Babel, e está escrito na Bíblia, Gênesis, capítulo X, que Cam, filho de Noé, gerou Nimrod, e que este se tornou um homem forte como um gigante e que foi um grande rei.

E o início de seu Reino foi o do verdadeiro Reino de Babilônia, de Arach e Archad e Calan e da Terra de Senaar.

E este mesmo Nimrod começou a construção da Torre da Babilônia, e ensinou a seus trabalhadores a arte da medida, e tinha muitos construtores, mais de quarenta mil.

E ele os amava e os tinha em grande estima.

E isto está escrito no Polycronicón e em outras Histórias e, em parte, testemunhado na Bíblia, no Gênesis, capítulo X, onde se estipula que Asur, que era um parente próximo do Nimrod saiu da Terra de Senaar e construiu a cidade de Nínive e de Plateas e muitas outros, e assim diz: “De Terra illa i de Sennam egressus est Asure et edificavit Nunyven et Plateas civitatis et Cale et Jesen quoque inter Nunyven et hec est civitas magna”.

A razão exige que digamos abertamente como e de que forma foi fundado o ofício da construção, e quem foi o primeiro a dar-lhe o nome de Maçonaria.

E você deveria saber o que é dito e escrito no Polycronicón e em Metodio, bispo e mártir, que Asur, que foi digno senhor de Senaar, solicitou ao Rei Nimrod que lhe enviasse pedreiros e operários do Ofício que lhe pudessem ajudar a construir a cidade que desejava edificar.

E Nimrod lhe enviou trezentos maçons.

E quando deviam partir, ele os chamou diante de si e lhes disse: “Vocês devem se apresentar diante de meu primo Asur para ajudá-lo a construir uma cidade, mas velem para que seja bem dirigida; vou lhes dar um encargo proveitoso para vocês e para mim.

Quando chegarem diante deste Senhor, procurem ser tão leais a ele quanto o são a mim; façam, como se fossem irmãos e permaneçam lealmente unidos; e aquele que têm maior capacidade ensine a seu companheiro e o impeça de se voltar contra seu Senhor, para que assim eu possa receber o mérito e o agradecimento por tê-los enviado a ele, e por ter-lhes ensinado a Arte. ”

E eles receberam o encardo de seu patrão e Senhor e chegaram diante de Asur e construíram a cidade de Nínive, no país de Plateas, e outras cidades entre Cale e Nínive.

E assim, a Arte da construção foi engrandecida e imposta como ciência.

Nossos primeiros antepassados, os maçons, tiveram esta responsabilidade, como está escrito nos nossos Deveres, e também como já vimos escrito em francês, em latim, e na história de Euclides; mas agora diremos de que maneira Euclides veio a adquirir conhecimentos de geometria, assim como está escrito na Bíblia e em outras histórias.

No capítulo 12 do Gênesis diz-se que Abraão chegou à terra de Canaã e que o Senhor lhe apareceu e disse: “Eu darei esta terra a ti e teus descendentes”, mas houve uma grande fome sobre a Terra e Abraão tomou Sara, sua esposa, consigo e partiu para o Egito em peregrinação, e enquanto durou a escassez eles permaneceram ali.

E Abraão, como diz a Crônica, era um homem sábio e um grande Doutor e conhecia as sete ciências e ensinou aos egípcios a Ciência da Geometria.

E este digno Sábio Euclides foi seu aluno e aprendeu com ele.

E eles deram pela primeira vez o nome de Geometria, porque antes não tinha este nome.

Assim, diz-se no Ethimologiarum de Isidoro, no livro 5, capítulo I, que Euclides foi um dos fundadores da Geometria, e que lhe deu este nome porque naquele tempo havia um rio no Egito, o Nilo, que cresceu até tal ponto na terra que os homens não podiam habitá-la.

Por isso, este digno estudioso, Euclides, os ensinou a fazer grandes paredes e valas para reter a água e eles, com a geometria, mediram a terra e a dividiram em muitas partes, e cada um fechou sua parte com paredes e valas, e por isso a terra se tornou fértil e deu a todos os tipos de frutas e jovens, homens e mulheres, mas eram tantos os jovens que não podia viver bem.

E os governantes, senhores do país, reuniram-se no Conselho para ver como ajudar a seus filhos que eles não tinham encontrado sustento.

E neste Conselho estava este digno Douto Euclides, e quando viu que não podiam decidir sobre o assunto, lhes disse: “Tomem seus filhos e coloquem-nos sob o meu comando, e eu lhes ensinarei uma ciência tal que viverão com ela dos Senhores, sob a condição de jurar que me serão fiéis e eu farei isso por vocês e por eles.”.

E o Rei e todos os Senhores o garantiram.

E eles conduziram seus filhos diante de Euclides para que ele os guiasse ao seu critério, e ele lhes ensinou esta Arte, a Maçonaria, e lhes deu o nome de Geometria, devido à divisão do terreno que havia ensinado ao povo no tempo da construção dos muros e fossos, e Isidoro disse no Ethimologiarum que Euclides a chamou Geometria.

E ele lhes deu o dever de chamar Companheiro uns aos outros, e não de outra forma, porque pertenciam a uma mesma arte e eram de sangue nobre e filhos de Senhores.

E que o mais habilidoso deveria ser o guia no trabalho e ser chamado Mestre, e lhes atribuiu outras tarefas que estão escritas no livro dos Deveres.

E assim eles trabalharam com os Senhores da Terra, e construíram cidades, castelos, templos e palácios.

Naquele tempo, os filhos de Israel que viviam no Egito aprenderam a arte da Maçonaria.

E logo, quando foram expulsos do Egito, chegaram à Terra de Behest, agora chamada Jerusalém.

E o Rei David iniciou a construção do Templo de Salomão.

O Rei David amava os Maçons, e lhes deu direitos que não tinham antes.

E na construção do Templo, nos tempos de Salomão, tal como referido na Bíblia, no 3º livro Regum, capítulo quinto, Salomão tinha oitenta mil construtores ao seu serviço.

E o filho de Tiro era seu chefe.

E em outras crônicas e em outros livros de Maçonaria diz-se que Salomão lhes confirmou a tarefa que Davi, seu pai, havia dado aos maçons.

E o próprio Salomão lhes ensinou em formas pouco diferentes daquelas utilizadas hoje.

E desde então esta importante ciência foi levada para a França e outras regiões.

Houve um tempo um digno Rei da França chamado Carolus Secundus, ou seja, Carlos II, e este Carlos foi eleito Rei da França pela Graça de Deus e por sua estirpe.

E este mesmo Rei Carlos era maçom antes de ser Rei e quando chegou a Rei amou os maçons e os teve em grande estima, e lhes deu deveres e regulamentos em conformidade com o seu plano, e alguns deles ainda estão em uso na França; e ele mesmo determinou que devessem se reunir em Assembleia uma vez por ano para falar entre si, Mestres e Companheiros, e para [decidir quem] havia de guiá-los e [para acertar] todas as coisas erradas.

E pouco depois Santo Adabelio chegou à Inglaterra e converteu Santo Albano ao Cristianismo.

E Santo Albano amava os maçons e lhes pela primeira vez os cargos e usos na Inglaterra.

E lhes ficou uma hora conveniente para lhes pagar pelo trabalho.

E depois houve um importante rei da Inglaterra chamado Athelstan e seu filho mais novo amava a Ciência da Geometria, e sabia bem que a arte manual do Oficio praticava a ciência da Geometria como os Maçons, e por isso os [reuniu] em Conselho e adotou a prática desta ciência na especulação, porque na especulação era mestre e amava a Maçonaria e os maçons.

E ele mesmo se fez Maçom e lhes deu cargos e nomes que ainda estão em uso na Inglaterra e em outros países.

E estabeleceu que [os Maçons] deveriam ser pagos razoavelmente por seu trabalho, e conseguiu um decreto do Rei que [sancionou], o direito de se reunir em Assembleia quando achassem que havia passado um período razoável e que viessem [escutar] seus Conselheiros, como está escrito e se ensinava no Livro de nossos encargos e deveres, pelo que deixo já o argumento.

Os homens de bem, por esta razão e desse modo, [fizeram com que] começasse a Maçonaria.

Ocorria às vezes, que os grandes senhores não tinham grandes posses, e assim não podiam ajudar seus filhos nascidos livres, porque tinham muitos e, portanto, se aconselharam sobre a forma como lhes podiam ajudar, e estabelecer que pudessem viver honestamente.

E os enviaram aos Sábios Mestres da importante Ciência da Geometria, para que eles, com sua sabedoria, pudessem dar aos filhos uma maneira honesta de viver.

Por isso, um deles, chamado Englet, que foi um sábio fundador muito inteligente, estabeleceu uma Arte e a chamou Maçonaria, e assim, com sua Arte, instruiu os filhos dos grandes Senhores, a pedido dos pais e com a livre vontade dos filhos; quando eles foram educados com grande cuidado, após um certo período, nem todos foram igualmente capazes, de forma que o referido Mestre Englet determinou que todos os que terminaram [a aprendizagem] com habilidade deveriam ser admitidos [no ofício] com honras, e chamou o mestre mais qualificado para instruir os mestres menos qualificados, e foram chamados mestres pela nobreza de seu engenho e por sua habilidade na arte.

Assim, a referida Artes, iniciada na terra do Egito, se espalhou de Terra em Terra, de Reino em Reino.

Depois de muitos anos, na época do Rei Athelstan, que foi rei da Inglaterra, seus conselheiros e de outros grandes senhores, de comum acordo, devido a graves culpas lançadas contra os maçons, estabeleceram certa regra para eles; uma vez ao ano, ou a cada três anos [se isso correspondia] aos desejos do rei e dos Grandes Senhores do País e do povo, de província em província, e de país em país, se reuniriam em Assembleia todos os maçons e companheiros da referida Arte, e em tais reuniões os mestres seriam examinados sobre os artigos [da Constituição], que foram logo escritos e se estabeleceu que fosse verificado se os mestres eram capacitados e habilitados, em benefício de seu Soberano e para honrar sua Arte.

E, além disso, foi estabelecido que devessem cumprir bem seu encargo de empregar os bens, grandes ou pequenos, de seus senhores, porque deles recebiam o pagamento por seu serviço e seu trabalho.

O primeiro artigo é o seguinte: Que cada mestre desta arte deve ser sábio e leal ao Senhor a quem serve; e não pagar a nenhum trabalhador mais do que ele pense que seja merecido, distribuindo seus benefícios realmente como gostaria que fossem distribuídos os seus, depois de ter [levado em conta] a escassez de grãos e alimentos no país, e não prestando quaisquer favores, para que todos possam ser remunerados de acordo com o seu trabalho.

O segundo artigo é o seguinte: Que cada mestre desta arte deverá ser informado antes de entrar em sua Comunidade; que sejam [recebidos] como convém; que não possam ser desculpados [por sua ausência], senão somente por algum motivo [válidos].

Mas se forem considerados rebeldes [diante de] tal Comunidade, ou culpados de qualquer forma, de danos aos próprios Senhores, os autores nesta Arte não serão perdoados de forma alguma, [e serão julgados e será verificada] sua expulsão, e quando se encontrarem [em perigo de morte], [ou enfermos], sem risco de morte, o mestre que seja o chefe da Assembleia [quem o deve julgar] será avisado.

O terceiro artigo é este: que nenhum mestre tome um aprendiz por um período inferior a sete anos, pelo menos, porque, em um período mais curto, não pode chegar adequadamente à sua Arte e, portanto, não será capaz de servir fielmente ao seu Senhor, e de compreender [a Arte] como um Maçom deve compreendê-la.

O quarto artigo é este: que nenhum mestre tome para educar, sem proveito qualquer aprendiz ao qual esteja ligado por vínculos de sangue, já que, devido ao seu Senhor, a quem está ligado, o desviará de sua Arte e poderá chamá-lo diante de si fora de sua Loja e do lugar onde trabalha; porque seus companheiros talvez lhe ajudem e lutem por ele, e aqui poderia surgir um homicídio, o que é proibido, e também devido a que sua arte começou com os filhos de grandes senhores, nascidos livres, como já foi dito.

O quinto artigo é este: que nenhum mestre envie seu aprendiz, durante o tempo de sua aprendizagem a outro, pois nenhum benefício pode advir disso, e embora pense que pode agradar a seu novo Senhor, o mais importante é o benefício que o Senhor poderá obter do lugar onde foi treinado em seu ensino.

O sexto artigo é o seguinte: que nenhum mestre, por ganância ou proveito, tome aprendizes para lhes ensinar coisas imperfeitas, e que tenham mutilações e, portanto, não possam realmente como deveriam.

O sétimo artigo é o seguinte: Que nenhum mestre seja visto ajudando ou protegendo, ou sendo o sustento de qualquer ladrão noturno, pelo qual [por causa do roubo] seus companheiros não possam cumprir com o trabalho diário e não possam se organizar.

O oitavo artigo é o seguinte: Que não ocorra quer qualquer Maçom que seja perfeito e hábil venha buscar trabalho e encontre um modo de trabalhar imperfeito e incapaz; o mestre do lugar receberá o maçom perfeito e dispensará o imperfeito em benefício de seu Senhor.

O nono artigo é o seguinte: que nenhum mestre assumir o lugar de outro, porque foi dito na arte da construção, que ninguém deverá terminar um trabalho iniciado por outro, em benefício de seu Senhor; assim, quem já o começou [tem o direito de] acabar ao seu próprio modo, e sejam quais forem os seus métodos.

Esta resolução foi adotada por vários senhores e mestres de diversas províncias e Assembleias de Maçonaria, e diz o seguinte:

O primeiro ponto: é necessário que todos os que desejam ser Companheiros da referida arte Jurem por Deus, pela Santa Igreja e por todos os Santos, diante de seu mestre e seus Companheiros e irmãos.

O segundo ponto: ele [o companheiro] deve cumprir seu trabalho diário, em virtude do que lhe foi pago.

O terceiro ponto: ele [deve aceitar] as decisões dos seus companheiros em Loja e em Câmara e em qualquer outro lugar.

O quarto ponto: Não enganará a sua Arte, nem a prejudicará, ou sustentará afirmações contra a Arte ou contra alguém da Arte, senão que os manterá com dignidade porque ele pode.

O quinto ponto: Quando receba seu pagamento, o tomará humildemente, já que o mestre estabeleceu o tempo do trabalho e o resto (por ele) ordenado está permitido.

O sexto ponto: Se surgir qualquer discórdia entre ele e seus companheiros deverá obedecer humildemente e permanecer às ordens do mestre, ou na sua ausência, ao vigilante [nomeado] pelo mestre; e na próxima festa religiosa se colocará à disposição dos Companheiros; não em um dia útil, deixando o trabalho e o proveito de seu Senhor.

O sétimo ponto: Que não deseje a esposa ou a filha de seu mestre ou de seus companheiros, e se for casado, não tenha amante, porque poderiam surgir divergências entre eles.

O oitavo ponto: se acontecer de ser nomeado vigilante por seu mestre, que seja um transmissor seguro entre seu mestre e seus companheiros, e na ausência de seu mestre, substituindo-o com empenho, para a honra do mestre e vantagem do Senhor a quem serve.

O nono ponto: se for mais sábio e agudo que o companheiro que trabalha com ele na Loja ou em qualquer outro lugar, e se perceber que o outro deve deixar a pedra sobre a qual está a trabalhar por falta de habilidade, deverá instruí-lo para que o amor cresça entre eles e a obra do senhor não seja perdida.

Sobre a Assembleia de Justiça.

Quando o Mestre e os Companheiros sejam avisados e chegam a tais Assembleias, se for preciso serão convidados a participara junto com os companheiros e o mestre da Assembleia, o xerife do condado, o prefeito da cidade, e o conselheiro mais antigo da Cidade onde se celebra a Assembleia, para servir de ajuda contra os rebeldes e para manter o direito do Reino.

Em princípio [entram no Ofício] homens novos que nunca foram condenados, de modo que não sejam nunca ladrões, ou [cúmplices] de ladrões, e que desenvolvam seu trabalho diário pela recompensa que recebem de seu Senhor, e deem um verdadeiro resumo a seus Companheiros das coisas que devem ser explicadas e escutadas, e os amem como a si mesmos.

E devem ser leais ao Rei da Inglaterra e ao Reino, e ater-se com todas as suas forças aos artigos mencionados.

Depois disso será perguntado se algum mestre ou companheiro que tenha sido instruído infringiu algum artigo e ali se estabelecerá se nunca fez tais coisas.

Por isso, vale dizer, se algum Mestre ou Companheiro que tenha sido avisado [da acusação], antes de vir a tal Assembleia, se rebela e não comparece, ou ainda tenha transgredido algum artigo, se isso for demonstrado, deverá renegar sua qualidade de membro da Maçonaria, e não poderá, jamais, usar sua Arte.

E se ousar praticá-la, o Xerife do país em que for encontrado trabalhando deverá colocá-lo na prisão e colocar todos os seus bens nas mãos do Rei até que seja mostrada e concedida a graça.

Por este motivo, [os participantes] nesta Assembleia estabeleceram que tanto o mais baixo quanto o mais alto deve ser fiel servidor de sua Arte em todo o Reino da Inglaterra.

Amém.

Assim seja.

JESUITAS BRETÕES NA FONTE DA MAÇONARIA FRANCESA?

Tradução José Filardo

por Francis Moray

Um dos “quadros de missão” jesuítas usados no final do século XVII – Antes do advento da Maçonaria Moderna

Jesuíta! Maçom! Dois termos raramente associados – exceto pelos adeptos das fantasias complotistas ou um Umberto Eco no Cemitério de Praga. Duas palavras raramente associadas, certamente, mas a quantidade de elementos que sugerem que seria preciso – e até provável – desenterrar a questão das ligações – reais ou imaginárias – entre a Maçonaria e Companhia de Jesus.

Com frequência, nos recantos mais obscuros da Maçonaria – obscuros porque menos explorados – não é incomum ver a sombra dos jesuítas. Jesuítas que, antes de serem rebatizados com esse nome, chamavam-se entre si de “companheiros” …

Certamente, a eventualidade de conexões reais entre jesuítas e maçons seria suficiente para irritar ambos os lados, que em parte esse site de busca quase deixa abandonada e esta história ainda está largamente por escrever. Deste ponto de vista, o estudo particular do eventual impacto que puderam ter os missionários da Companhia na Grã-Bretanha, nos séculos XVII e XVIII sobre a futura maçonaria em gestação, principalmente sobre a metodologia dos painéis de loja que não deixa de ressoar com nosso assunto.

Formar a sociedade de amanhã

Não é o caso de se concentrar aqui especificamente nos primórdios da maçonaria na Bretanha a partir do final do século XVII, que as obras de André Kervella em particular, puderam vir à luz (1). No entanto, para a pergunta diante de nós, já podemos destacar que um grande número de maçons ou seus filhos foram alunos de escolas jesuítas em Quimper, a primeira (inaugurada em 1621) e em Brest, aberta um pouco mais tarde (1686). No contexto particular desse balbucio da maçonaria, na virada dos séculos XVII e XVIII e nos primeiros anos deste último, a pedagogia e a metodologia (muito teatralizada) inacianas, pelo menos – se não a doutrina – não tiveram alguma influência sobre esses homens que estarão começando na sociedade de seu tempo? Certamente, nessa época, a Companhia de Jesus administrava uma parte considerável dos colégios e, assim, formou uma certa elite burguesa em toda a França (a nobreza se reservava mais à viril carreira das armas que aos jogos “amolecedores” do espírito). Mas é inegável que esta formação jesuíta se revestia de uma dimensão considerável na Bretanha e tanto mais, quanto à maçonaria, que esta pequena burguesia comerciante exercerá um poder significativo em torno do armamento dos portos e, portanto, no seio das primeiras lojas de Ponant.

Jesuítas de choque

Sem que eles a tenham realmente inventado em sua prática, os jesuítas elevaram especificamente a aculturação em princípio da ação e a estruturaram. A aculturação é a ideia de introduzir suas próprias filosofias em uma determinada terceira cultura, fingindo adotar essa última, de viver com as pessoas o mais próximo delas. Em suma, pode-se dizer que os asiáticos estarão entre os primeiros alvos desta aculturação, montar o tigre, esposar mais de perto as práticas de um povo para melhor o transformar.

No espírito da transformação e da aculturação, a Grande Obra dos jesuítas será a educação. Os jesuítas revelar-se-ão mestres em matéria de inovação e engenharia pedagógica. Para atingir os seus fins – o fim justifica os meios, diz o conhecido ditado jesuíta – eles se mostraram muito inovadores, mesmo revolucionários: por exemplo, grande novidade na época, as escolas jesuítas serão gratuitas e assim permanecerão até a supressão temporária da ordem em 1763.

Somente se os jesuítas proporcionavam uma atenção especial a esta população educada, potencialmente influente um dia, certamente entre eles, mesmo que não fossem a maioria, não se esqueciam das “pessoas pequenas”. Isso será especificamente o caso na Bretanha, que, como sabemos, tinha uma relação especial com a religião. “No século XVII, nossa Bretanha francesa foi completamente conquistada pelos hábitos jesuítas e o tipo de piedade do resto do mundo. Até então, a religião tinha tido um caráter absolutamente à parte “, escreveu Ernest Renan (2).

No centro deste dispositivo, encontramos uma personagem particularmente incomum, o padre jesuíta Julian Maunoir (1606-1683). Ar Tad Mad! O Bom padre! Maunoir, o Bendito (3)! Maunoir o exagerado. O homem do “Sempre mais! “. Um homem paradoxal, em todo caso, que é aquele a quem se odeia ou a quem se incensa, sem nuance. Mas não teria havido Maunoir sem seu mestre, Michel o Nobletz (1577-1652). Este tem um certo lado de João Batista, aquele do eremita exaltado pregando no deserto às multidões mais surpresas que fascinadas. Parafraseando João, 3: 30, existe no relacionamento Nobletz-Maunoir um eco da exclamação de Batista: “Era necessário que ele [Maunoir] crescesse e que ele [Nobletz] diminuisse. No binômio Nobletz-Maunoir, o primeiro será sem dúvida o inspirador enquanto o segundo será o mestre de obra. Esse último somente dará, ao todo, apenas uma magnitude especial para a “obra” nascida na mente de seu mestre. Nobletz havia limpado e arado; Maunoir semeará e colherá.

Os Taolennoù, ancestrais dos painéis de loja?

Há pouca informação sobre a vida de Michel Nobletz fora do âmbito da hagiografia de Maunoir, seu biógrafo. Mas o que vai especialmente chamar nossa atenção é sua “invenção” de um processo pedagógico original: o Taolennoù (4). Para edificar e atingir o espírito de uma população totalmente ignorante e propensa ao medo irracional, ele desenvolve, de fato estas ferramentas pedagógicas inovadoras com base em ilustrações, esses quadros de missão, um tipo de revista em quadrinhos próprios para impressionar da maneira certa de um “bom cristão”. Existem algumas dezenas desses quadros que ele criou e que podem ser divididos em duas categorias: a primeira declinava os temas mais facilmente compreensíveis: sobre o bem e o mal, os meios a encontrar e ganhar o Paraíso (ar Baradoz), as ameaças infernais … com nomes tais como a Vida de Nosso Senhor, quadros do Padre Nosso, do inferno, dos sete pecados capitais, da Paixão … A segunda categoria era de uma abordagem mais difícil com conteúdo muito mais esotérico, para não dizer herméticos como aqueles intitulados as Três árvores, o Cavaleiro errante, as Seis Cidades de Refúgio …

Não se pode deixar de notar uma semelhança real, tanto formal e gráfica quanto metodológica, entre estes “quadros de missão” pintado em couro, telas ou placas de madeira e os futuros painéis (ou tapetes) de Loja da maçonaria. Quase se poderia chegar a ver um paralelo entre o mais simples Taolennoù, da primeira categoria, e os painéis de lojas simbólicas (três primeiros graus da Maçonaria), e de outro lado, entre os mais complexos da segunda categoria e os altos graus da maçonaria na dimensão cavalheiresca. Além disso, tantos uns e quanto os outros estavam associados a catecismos elementares de perguntas e respostas. Seria fácil ver uma relação entre estes Talennouù e os painéis de lojas maçônicas. Especialmente considerando que a utilização destes últimos será primeiro uma prática continental mais que Anglo-Saxã (a Inglaterra não adotara verdadeiros painéis de loja a não ser muito mais tarde e ainda assim eles terão uma forma um pouco diferente).

Evangelização através de grandes espetáculos

Escarnecido, o idealista Nobletz, ar bellec for, o “padre louco” vai transformar o mundo todo. Maunoir, pragmático e estrategista, rapidamente compreendeu que os métodos de “ourives” de seu mentor o condenavam a um público limitado e que, se ele queria tocar o maior número, ele deveria passar a uma produção mais intensiva (em termos cinéfilos modernos, poderíamos dizer que de cinema de autor, ele optou pela realização de filmes de sucesso, e isso é exatamente o que ele vai fazer com suas encenações grandiosas). À “qualidade” de seu mestre, ele prefere a “quantidade”.

Foi a partir de 1640 que realmente vai começar o trabalho missionário de Maunoir. Ele cai na estrada. Nobletz legou-lhe seus Taolennoùs, seus cadernos “manuais”, seus livros, sua varinha (que Maunoir sabe como usar este instrumento cheio de poderes ‘mágicos’), seu sininho … Nobletz caminhava quase sozinho; Maunoir coloca-se à frente de um pequeno exército de sacerdotes (e até mesmo mulheres catequistas) dedicados à sua causa, tais como “cavaleiros errantes” (para citar o título de um dos Taolennoù mais enigmáticos quanto ao seu significado mais profundo). Por mais de 42 anos, o homem de “sempre mais” (segundo um de seus apelidos), não vai parar de evangelizar. Maunoir estrutura suas missões, que duram de três a quatro semanas, de maneira muito militar. Muito rapidamente, ele adquiriu um senso de encenação. Ele era cheio de achados litúrgicos, sabia usar e abusar de artifícios … E funcionava: ele atraía multidões, tanto como espectadores quanto colaboradores. Vinha-se tremer, se extasiar, cantar … e acessoriamente, orar. Mas o que se deve orar? O maravilhoso está em todos os lugares. Como no culto de antanho. Há aparições e milagres, mais ou menos encenados, doentes curados, surdos recobrando a audição, cegos a visão, mudos a fala, coxos o movimento … Tudo é feito para amortecer os espíritos, de forma rápida e forte, usando todos os truques da encenação emocional. Pierre-Jakez Helias, em seu famoso livro, O Cavalo do Orgulho descreveu o efeito dramático que os “quadros” [Taolennoù] do Padre Maunoir ainda produziam sobre uma criança do início do século 20.

No final de sua vida, quase mil sacerdotes o seguiam e em suas missões, ele é sempre acompanhado por vinte a quarenta assistentes. Com Maunoir, os números são na verdade muito rapidamente impressionantes. Em apenas um ano (1641), ele conta, teria realizado 3.000 conversões (ainda havia a quem converter em um país considerado católico a 99%?) e 40.000 pessoas educadas (e 1641 é apenas o começo de suas missões). No final de sua vida, em 1683, ele teria completado 439 missões, afetando mais de 400.000 pessoas. Se os números estão corretos, ele não podia deixar de ter um impacto sobre as populações bretãs – de influência ou rejeição, de admiração ou repulsa.

Embora muitas vezes o associemos a isso, Maunoir acabará por não ter usado muito os Taolennoùs exceto em um sentido de filiação emocional com Nobletz (5). Para Maunoir, os quadros permitiam metodologicamente apenas uma transmissão de informação a muitas poucas pessoas a cada vez. Mas ele reconhecia completamente o valor pedagógico, e de alguma forma, seus shows e encenações grandiosas são verdadeiros Taolennoùs ao vivo. Ele também deixou traços na paisagem Bretã, que também retomam o processo pedagógico dos “quadros”. Podemos pensar, assim, das esculturas do menir de Saint Uzec em Pleumeur-Baudou, cristianizado em 1674, durante uma missão de Maunoir, que são autênticos Taolennoùs de pedra … e que, mais uma vez, lembram surpreendentemente, incluindo os símbolos utilizados, os futuros painéis de loja.

Obviamente, na realidade, não é novamento possível estabelecer a filiação certa entre os “quadros de missão” e os painéis de loja. É possível apenas notar uma semelhança surpreendente de uso e forma. E há que se lembrar (especialmente se os jesuítas puderam integrar as fileiras da Maçonaria) de uma possível conexão entre os futuros utilizadores (ou designers) dos painéis de loja e sua educação jesuítica na Bretanha no auge da utilização maciça e espetacular dos Taolennoùs.

Notas:

1: em particular, estão nas origens da Maçonaria francesa: exilados britânicos e cavalheiros Bretões, 1680-1750, Edições do Priorado, 1996. A obra está prestes a ser relançada em uma versão revisada, ampliada e corrigida com o título, Maçonaria Francesa. Os precursores jacobitas na Bretanha (1689-1750), publicado pela Editora Pedra Filosofal.

2: Memórias da infância e juventude.

3: Declarado beatificado em 1951, depois de quase três séculos de lobby eclesiástico bretão para esta beatificação, tornando-o o apóstolo da Bretanha.

4: Em Bretão simplesmente “quadro”.

5: É principalmente outro jesuíta Vicente Huby (1608-1693), que vai usá-lo em sua casa de repouso em Vannes, mais para a formação de uma elite (não só religiosa).

Publicado 11 de janeiro de 2017 em http://www.fm-mag.fr/article/societe/des-jesuites-bretons-1419

A MAÇONARIA E A CONEXÃO ROSA-CRUZ

Autor: João Anatalino

A antiga Maçonaria

É comum á muitos maçons entrarem para os quadros da Maçonaria, freqüentar suas reuniões, ás vezes assumir todos os cargos em Loja, inclusive a venerança, galgar todos os graus do aprendizado maçônico e chegar ao fim dessa escalada com uma série de dúvidas sobre o que é, e o que significa, de fato, a Maçonaria.

Isso é um fato, e do ponto de vista da própria história da Maçonaria se justifica que seja assim. Isso porque sua história, por si mesma é uma amálgama das diversas conformações que a sociedade tem assumido desde que ela se organizou em grupos, depois em povos, nações e estados. De todas as estruturas sociais, desde as mais remotas, até as mais modernas, a tradição maçônica tem emprestado temas e incorporado ideias, as quais, se não analisadas no seu devido contexto, e colocadas no seu exato sentido, acabam mais por confundir do que esclarecer.

Historicamente, todo maçom sabe que a Ordem á qual ele pertence tem sua origem nas antigas corporações de ofício da Idade Média, especialmente aquelas que congregavam os pedreiros profissionais, construtores de igrejas e obras públicas. Esses profissionais, conforme informa Jean Palou em sua obra, eram homens livres, sábios formados no exercício de uma profissão que combinava a técnica operatória manual do ofício com o conhecimento da ciência das formas (geometria), e a mística do número (o pitagorismo).[1]

E assim, somente eles, detentores de um conhecimento considerado sagrado, poderiam construir as grandes catedrais, de acordo com a idéia que se tinha desses monumentos, ou seja, que deveriam ser construídos de uma certa maneira, ao mesmo tempo mística (capaz de atrair os influxos da benevolência divina) e prática, que era a de servir a uma finalidade social, catalisando e aglutinando as forças da comunidade. Por isso Fulcanelli, ao se referir á catedral medieval, diz: “Santuário da Tradição, da Ciência e da Arte, a catedral gótica não deve ser olhada como uma obra unicamente dedicada ao cristianismo, mas antes como uma vasta coordenação de idéias, de tendências, de fé populares, um todo perfeito ao qual nos podemos referir sem receio desde que se trate de penetrar o pensamento dos ancestrais, seja qual for o domínio: religioso, laico, filosófico ou social. Se há quem entre no edifício para assistir aos ofícios divinos, se há quem penetre nele acompanhando cortejos fúnebres ou os alegres cortejos das festas anunciadas pelo repicar dos sinos, também há quem se reúna dentro delas noutras circunstâncias. Realizam-se assembléias políticas sob a presidência do bispo; discute-se o preço do trigo ou do gado; os mercadores de pano discutem ai a cotação dos seus produtos; acorre-se a esse lugar para pedir reconforto, solicitar conselho, implorar perdão. E não há corporação que não faça benzer lá a obra prima do seu novo companheiro e que não se reúna uma vez por ano sob a proteção do santo padroeiro”[2].

Esses profissionais da construção civil, construtores de catedrais eram conhecidos como pedreiros-livres, ou na gíria da época, maçons, ou seja, o artesão do maço e cinzel, que registravam na pedra bruta os ideais ascéticos de uma sociedade que tinha no misticismo de suas tradições os principais alicerces de suas crenças.

Mas um recenseamento das tradições, usos e costumes da velha Maçonaria operativa (se isso fosse possível), não seria suficiente para esclarecer como essas antigas corporações de oficio medievais se transformaram em clubes de cavalheiros, filósofos e agitadores políticos, que em fins do século XVI e pelos séculos seguintes iriam escrever, principalmente pela ação de seus membros, importantes capítulos da história da sociedade ocidental.

O legado da alquimia

Poucos episódios da história universal foram tão decisivos em termos de mudança de conceitos e comportamentos quanto o movimento desencadeado pelo frade alemão Martinho Lutero, conhecido como Reforma Protestante. Esse movimento, não só gerou radicais mudanças no pensamento dos povos ocidentais, como também ensejou profundas modificações sociais e políticas na sociedade, liberando o pensamento humano para a criação de institutos e práticas que antes o pensamento religioso oficial reprimia e condenava.

Uma dessas práticas, cujo apelo místico, e ao mesmo tempo romântico e utópico, causava forte atração aos espírito investigativo dos intelectuais medievais era a alquimia. Os trabalhos de René Alleau e Mircea Eliade demonstraram com muita propriedade que a alquimia, desde a mais remota antiguidade, sempre foi uma arte iniciática, associada aos mistérios da natureza.[3] Por isso era praticada pelos sacerdotes egípcios e hindus em seus templos, não só como forma operativa de produção de artefatos preciosos, mas também como disciplina do espírito para atingir o êxtase espiritual. Mais tarde, os filósofos taoístas e gregos a elevaram á nível de disciplina acadêmica, organizando-lhe uma epistemologia própria, fazendo dela uma arte especulativa e empírica ao mesmo tempo. [4]

No Egito essa arte era própria dos ourives, mestres na fabricação do “ouro falso”, como eram chamados os artefatos fabricados com metais comuns, submetidos a banhos dourados para imitar o ouro. Essa atividade era praticada sob a supervisão direta dos sacerdotes e tida como “arte sagrada”, comparável á arquitetura. 

Durante muitos séculos os gregos tentaram descobrir o segredo de tais banhos, e foi no curso dessas tentativas que eles desenvolveram a forma operativa da alquimia, especulando primeiro e depois realizando experiências de laboratório, anotando e analisando os resultados. Com isso deram á essa prática, em princípio uma arte empírica, um caráter de ciência experimental.

Trazida para a Europa pelos árabes, a alquimia se tornou uma ciência experimental, praticada por filósofos naturalistas, em sua maioria, monges confinados á Ordens religiosas e mosteiros, que no processo de fabricação dos produtos que necessitavam para suas vidas diárias, acabavam misturando a mística de suas crenças com as descobertas naturais que faziam em suas experiências práticas. Daí o caráter religioso-científico que a alquimia assumiu na Idade Média e a desconfiança que essa prática provocava nas autoridades religiosas.

A Reforma protestante

Com a reforma religiosa desencadeada por Lutero, a alquimia foi uma das práticas que escapou das amarras que a Igreja medieval lhe colocava e ganhou adeptos entre os espíritos esclarecidos da época, provocando uma verdadeira febre espiritual nos meios culturais da sociedade ocidental. Em toda a Europa, não havia príncipe, nobre, autoridade eclesiástica ou mesmo cidadão abastado que não tivesse um alquimista entre os integrantes do seu mecenato. Para todos esses cidadãos, financiar os trabalhos de um “mestre” nas artes herméticas, era a esperança de obter riqueza (transformando metais comuns em metais nobres) ou de realizar outros sonhos quiméricos como descobrir o elixir da longa vida, ou remédios e poções milagrosas capaz de curar doenças, ferimentos de guerra, ou ainda outros produtos que pudessem realizar lucro para seus financiadores.

Para muitos praticantes e financiadores de alquimistas, porém, era o apelo espiritual que a arte de Hermes continha que atraia a sua atenção para essa prática. Era um apelo que tinha muito a ver com as ideias e as esperanças trazidas pela Reforma Protestante, de um mundo melhor, livre da dogmática limitadora da Igreja de Roma. E foi na esteira desse pensamento liberalizante que nasceu o movimento que ficou conhecido como Rosa- Cruz.

A conexão Rosa-Cruz

Uma das melhores explicações dos motivos de alquimia ter se casado tão bem com as expectativas dos intelectuais reformistas nos foi dada pelo médico e filósofo Carl Gustav Jung. Um de seus mais importantes trabalhos tem por tema exatamente a alquimia. Nessa obra, o famoso psicanalista suíço desenvolve a idéia dos arquétipos, fazendo uma ponte entre o delírio alquímico e as ansiedades do inconsciente humano para alcançar a realização de seus sonhos. Para Jung, a alquimia seria uma técnica que procura desenvolver, operativamente, o mesmo processo que o inconsciente humano se utiliza para promover o desenvolvimento psicológico do homem. Com esse trabalho ele estabeleceu um elo entre o pensamento mágico e a psicologia, mostrando que existe uma clara interação entre esses dois domínios cerebrais, que só podem ser entendidos se estudados em conjunto.

Dessa forma, segundo Jung, a arte dos “filhos de Hermes”, como tais eram chamados os alquimistas, provinha de um conjunto de conceitos universais, compartilhados pelo Inconsciente Coletivo da humanidade desde tempos imemoriais, pois se fundamentava em mitos, símbolos, alegorias e sensibilidades que sempre existiram no psiquismo da espécie humana, e que se revelava em sonhos, intuições, crenças, superstições e folclores, muitas vezes inexplicáveis pelo crivo da razão, mas muito fortes nas bases estruturais do nosso espírito.

A alquimia era a arte das transmutações. Através da manipulação de certo tipo de matéria prima, os alquimistas pensavam poder descobrir o segredo que permitia á natureza realizar a transformação física dos metais. Daí a alquimia ficar conhecida como a técnica que permitia a transmutação de metais comuns, como o estanho e o chumbo, em ouro. Ao mesmo tempo, o operador alquímico, ao penetrar na intimidade da natureza e desvelar os seus segredos, ia também adquirindo uma consciência superior que lhe permitia uma elevação espiritual ao nível de uma experiência transcendental. Foi essa ideia, trabalhada em forma de crença, que os fundadores do movimento Rosa-Cruz divulgaram pelo mundo intelectual da época, causando uma grande ebulição espiritual, pois essa era exatamente a esperança que acalentava a alma da maioria das pessoas que sonhavam com utopias, e viam nas novas ideias que o Renascimento cultural e a Reforma religiosa haviam trazido.

A Maçonaria e a Rosa-Cruz

A fraternidade dos Irmãos da Rosa-Cruz foi um movimento formado por um grupo de pensadores herméticos que em fins do século XVI e início do século XVII causaram uma grande comoção nas estruturas do pensamento ocidental com suas construções especulativas utópicas, fundamentadas no seu saber alquímico.[5] Serge Hutin, escrevendo sobre esses místicos filósofos da utopia alquímica , diz que “eles constituem a coletividade dos seres elevados ao estado superior á humanidade vulgar, possuindo dessa forma os mesmos caracteres interiores que lhes permitem reconhecer-se entre si”.[6]

É, portanto, na esteira do pensamento Rosa-Cruz que podemos encontrar as sementes da Maçonaria moderna. Ambas são fruto da Reforma religiosa, pois saíram da mesma árvore que procurava integrar a espiritualidade do labor humano na sua luta para ganhar a vida com a ciência que ele adquire na interação do seu pensamento com a natureza que lhe fornece os meios para esse resultado. 

A idéia de uma sociedade internacional, circunscrita a alguns homens puros e de bons costumes, ligados pelo amor á virtude e a beleza, transformados por uma prática iniciática, era a proposta dos Rosa-Cruzes, como se depreende dos textos de seus dois mais importantes manifestos, Ecos da Fraternidade e Confessio Fraternitatis. [7]

Essa é, igualmente, a pregação de todos os doutrinadores maçons. A ciência maçônica, tal como a alquimia, também é a ciência das transmutações. Ela permite a transformação do próprio espírito do iniciado no sentido de se atingir uma etapa mais desenvolvida, seja no terreno da moralidade exotérica, seja no domínio da plenitude espiritual, esotérica. Essa transmutação, a nível filosófico, é a mesma experimentada pelo alquimista, na sua busca pela pedra filosofal, ou pelo cientista moderno na sua procura por uma explicação racional dos fenômenos da natureza. Como dizem Pawels e Bergier, “estamos numa época em que a ciência, no seu termo máximo, atinge o universo espiritual e transforma o espírito do próprio observador, situando-o num nível diferente do da inteligência cientifica, tornada insuficiente. Aquilo que acontece nos corações dos nossos atomistas é comparável á experiência descrita pelos textos alquímicos e pela tradição rosa-cruz.” [8]

Isso é o que os nossos antigos irmãos, que transformaram a Maçonaria dos pedreiros medievais em um movimento filosófico-ativista, estavam esperando que acontecesse no espírito do maçom que realmente compreendesse o valor e a finalidade da sua Arte. Ou seja, se para os alquimistas o corolário da sua obra era a pedra filosofal, para o maçom, a pedra filosofal seria o seu próprio espírito aperfeiçoado e pronto para realizar uma revolução social que transformasse o mundo imperfeito da época (metal impuro) em um mundo perfeito (a utopia social). Em outras palavras, uma verdadeira alquimia social.

A realidade e o sonho

Esse era o sonho dos nossos antigos irmãos que deram corpo e vida á Maçonaria moderna. Porém, o apelo romântico e esotérico que tanto atraia os espíritos dos nossos antigos irmãos para o exercício de uma alquimia social desapareceu com as exigências do pensamento moderno, que exige mais ação prática no terreno da política, da economia, da sociologia e das ciências que garantem o nosso viver diário. Por isso a arte do maçom, antes umbilicalmente ligada a ideia utópica que ligava a ascese espiritual do antigo construtor de catedrais com a esperança mística do operador alquímico, transformou-se em uma cadeia difusa (e confusa) de ensinamentos temáticos que buscam fazer do maçom um homem preparado para as exigências da vida moderna. O que nem sempre ( e diríamos raramente) é conseguido.

Assim é que encontraremos nos modernos rituais maçônicos uma profusão de alusões a padrões culturais antigos e modernos, encadeados, ás vezes, sem método ou direcionamento, mas que sempre podem ser recenseados em momentos importantes da história da humanidade. São resquícios de práticas e ensinamentos que deixaram marcas profundas na psique humana, e que constituem, como dizia Jung, um arsenal de arquétipos, que afinal, são a base do que chamamos de cultura humana. Tais são os conceitos de justiça, fraternidade, igualdade, liberdade, virtude, civismo, filantropia, compromisso e dignidade, que tanto aparecem nas cartilhas que veiculam o ensinamento maçônico. Padrões esses de interpretação variável ao longo dos tempos, e que são valorados segundo as necessidades e a vontade de quem detém o poder. Uma das funções da Maçonaria seria, portanto, funcionar como um filtro desses valores, conservando o seu padrão de pureza e virtude, o que, infelizmente, nem sempre consegue. Dessa forma, o sonho perde-se na realidade da vida, e o apelo emocional de uma prática que já encantou os espíritos mais nobres acaba se tornando uma tradição vazia de sentido que só continua atraindo pelos ecos de um passado glorioso.

Historicamente, portanto, a Maçonaria hoje, nada mais é do que uma emulação do antigo pensamento Rosa-Cruz, adaptado ás exigências modernas e despido do romantismo e do apelo místico que lhe davam os nossos precursores. Embora alguns maçons ainda estejam imbuídos do velho espírito dos Irmãos da Rosa-Cruz, que acreditavam poder transformar o mundo pela luz dos seus espíritos e pelo poder dos seus conhecimentos, é de se reconhecer que essa virtude, hoje, é dificilmente encontrável em nossas Lojas.

Mas tudo que um dia existiu pode ser recuperado. Como dizem Pawels e Bergier, quem sabe, um dia chegue um tempo em que os tempos se reencontrem.[9]

________________ 

[1] Maçonaria Simbólica e Iniciática, pg. 2

[2] Fulcanelli- O Mistério das Catedrais, pg. 50.

[3] Mircéa Eliade - Ferreiros e Alquimistas – Ed. Flammarion,1977

[4] Bernard.Rogers- Descobrindo a Alquimia pg. 28

[5] Vide, a esse respeito, Giordano Bruno e a Tradição Iniciática e O Iluminismo Rosa-Cruz, de Frances Yates, publicados, ambos pela Ed. Cultrix. Na imagem, Francis Bacon, filósofo e alquimista inglês, (1561 — 1626) que é tido como o fundador da ciência moderna. Sua filosofia pregava o exercício da ciência em favor do progresso da humanidade. Sua principal obra filosófica, “Novum Organum” é considerada uma das principais influências para o movimento intelectual que resultou na Maçonaria moderna. Foi participante ativo do movimento Rosa-Cruz.

[6] Serge Hutin . História da Alquimia. São Paulo, Cultrix, 1987.

[7] Bernard Gorceix- A Bíblia dos Rosa-Cruzes, Ed. Pensamento, 1970

[8] O Despertar do Mágicos, pg. 53.

[9] Idem -O Despertar dos Mágicos- pg 106